> For the complete documentation index, see [llms.txt](https://book.7988888.xyz/llms.txt). Markdown versions of documentation pages are available by appending `.md` to page URLs; this page is available as [Markdown](https://book.7988888.xyz/eeg/fft.md).

# 脑电分析之频谱分析

本文首发在个人博客上（[**7988888.xyz**](https://7988888.xyz/)**），此文章中所有链接均通过博客进行访问。**

**在上篇推送小波分析教程时，小编其实觉得在学习小波变换前，一定要了解的是傅里叶变换，这是学习变换的鼻祖。傅里叶变换相比于小波变换要简单一些，傅里叶变换主要能做到的是信号的频谱分析。**

**傅里叶当时提出的中心思想是：“任何周期函数都可以表示为周期复指数函数的无穷和\***\*。**”在当时，这是有争议的，另一位很有名的数学家拉格朗日也提出：**“正弦曲线无法组合成一个带有棱角的信号”\*\*。的确如此，正弦曲线的确在组合棱角信号时是无法拟合完全的，但是可以无限的逼近。

![img](https://tva1.sinaimg.cn/large/007S8ZIlgy1ggt4vcqr14j30bf06nmxb.jpg)

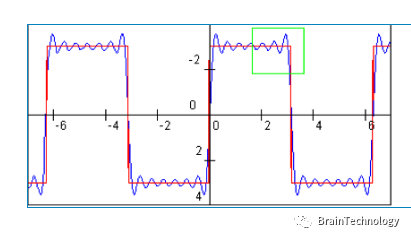
**在科学发展进程中，所以后人在原来的基础上进行了扩展：满足一定条件的函数可以表示成三角函数(正弦和/或余弦函数)或者它们的积分的线性组合。**

**为什么要进行傅里叶变换？**

**傅里叶变换是描述信号的需要。只要能反映信号的特征，描述方法越简单越好!信号特征可以用特征值进行量化。所谓特征值，是指可以定量描述一个波形的某种特征的数值。全面描述一个波形，可能需要多个特征值。傅里叶变换算法利用直接测量到的原始信号，以累加方式来计算该信号中不同正弦波信号的频率、振幅和相位。**

![img](https://tva1.sinaimg.cn/large/007S8ZIlgy1ggt4vgkq4dj30hk0a40t7.jpg)

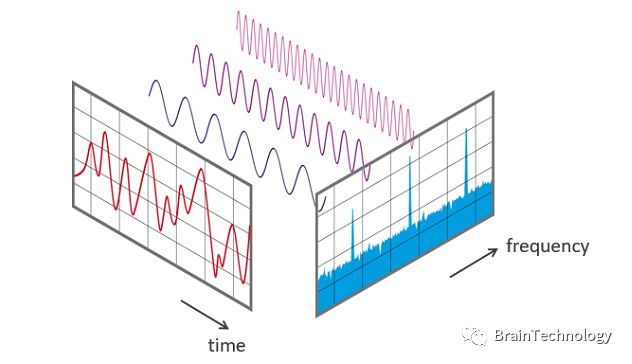
**图：信号在时域上和频域上的直观表示 ——来源网络**

![img](https://tva1.sinaimg.cn/large/007S8ZIlgy1ggt4vz45cnj30ln06wgmf.jpg)

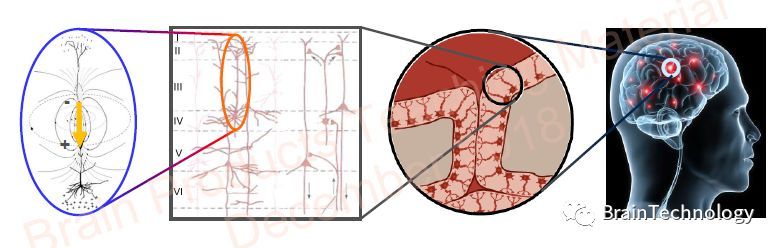
**在神经信号振荡中，快速傅里叶变换得到了极大的应用。**

**快速傅里叶变换 (fast Fourier transform),是利用计算机计算离散傅里叶变换（DFT)的高效、快速计算方法的统称，简称FFT。快速傅里叶变换是1965年由J.W.库利和T.W.图基提出的。采用这种算法能使计算机计算离散傅里叶变换所需要的乘法次数大为减少，特别是被变换的抽样点数N越多，FFT算法计算量的节省就越显著。——CSDN**

**EEG采集设备对波形进行采样，然后将采样转换为离散的值。 因为发生了转换，传统上的傅里叶转换在这些数据上无法进行。于是可以使用离散傅立叶变换(DFT)，其结果是离散形式的频域信号。 FFT是DFT的一种优化实现，计算量较少，但是本质上是对信号特征的提取。**

**在EEG信号来源中，推荐一篇文章《Where Does EEG Come From and What Does It Mean?》Michael X Cohen**，在这篇文章中能了解EEG信号振荡的神经元来源。从文章中可以知道我们通过EEG设备记录下来的EEG信号，是神经元振荡信号的集合。

**在前人的研究中，目前将脑电信号频率，按照频率大小分为Delta、Theta、Alpha、Beta and gamma。**

![img](https://tva1.sinaimg.cn/large/007S8ZIlgy1ggt4x9ks57j30dg094t9b.jpg)

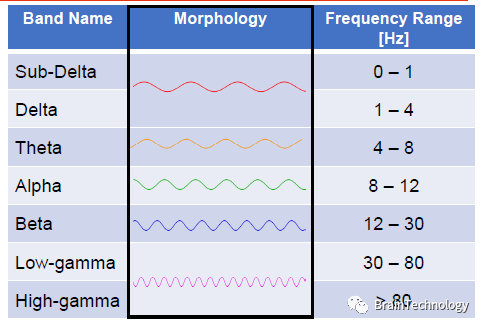
**但是，我们记录下来的原始信号属于时间-振幅的电压信号，并非是频率信号，我们在后期分析中想要把普通的幅度信号转换成频率信号，那么在分析上会采用快速傅里叶变换进行数据的转换。**

**在快速傅里叶变换中，为采样得到的数字信号N个采样点，经过FFT之后，就可以得到N个点的FFT结果。为了方便进行FFT运算，通常N取2的整数次方。**

**在Analyzer软件中输出值，有下面四种类型：**

![img](https://tva1.sinaimg.cn/large/007S8ZIlgy1ggt4xg6jy5j30kn04nq38.jpg)

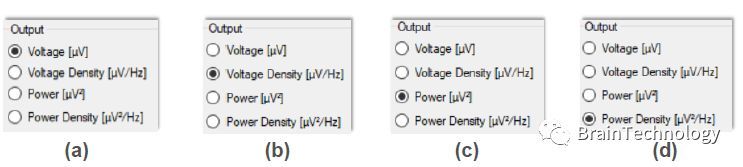
**a）频谱振幅**

**b）特定频率下的谱振幅密度（Δf：频率分辨率）**

**c）频谱功率**

**d）特定频率下的频谱功率密度（Δf：频率分辨率）**

**在FFT中有两个非常重要的参数—频谱分辨率和加窗函数。**

**频谱分辨率所定义的公式：Δf = fs/N**

**其中，fs为采样频率（sampling frequency）,N为FFT的点数。Δf代表FFT频率轴上的频率取值的间隔。**

**在Analyzer软件中的FFT模块中，会涉及到resolution的设置，在这里的设置理应为2的次幂为最优选择，这是做FFT分辨间隔所引起的。合理的分辨间隔将减少频谱的泄露，差的分辨率将导致频谱泄露。例如：**

![img](https://tva1.sinaimg.cn/large/007S8ZIlgy1ggt4xk4farj30kk06smxr.jpg)

![img](https://tva1.sinaimg.cn/large/007S8ZIlgy1ggt4xn6n6rj30kp062q3d.jpg)

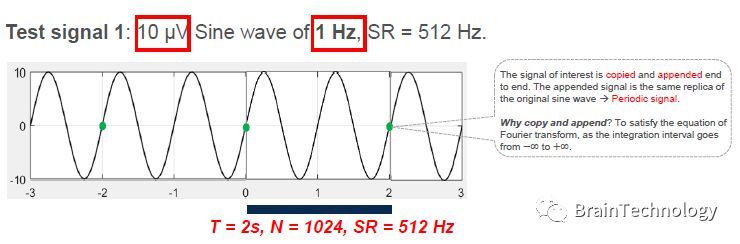
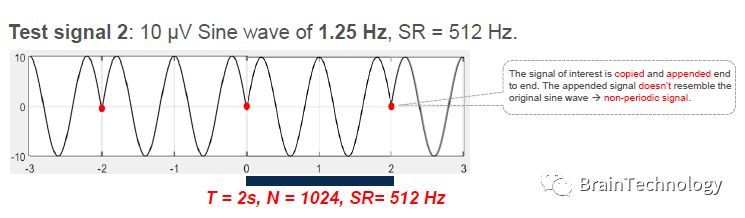
**不同的频率造成的模拟波形是不一样的，在节点处就会造成频谱泄露。**

**如何处理频谱泄露？**

**加窗函数。**

**在FFT界面，软件提供了两种加窗函数的使用。**

**摘自网络：“窗的波形图显示了窗本身为一个连续的频谱，有一个主瓣，若干旁瓣。 主瓣是时域信号频率成分的中央，旁瓣接近于0。 旁瓣的高度显示了加窗函数对于主瓣周围频率的影响。 对强正弦信号的旁瓣响应可能会超过对较近的弱正弦信号主瓣响应。 一般而言，低旁瓣会减少FFT的泄漏，但是增加主瓣的带宽。 旁瓣的跌落速率是旁瓣峰值的渐进衰减速率。 增加旁瓣的跌落速率，可减少频谱泄漏。”**

**“Hamming窗和Hanning窗都有正弦波的外形。 两个窗都会产生宽波峰低旁瓣的结果。 Hanning窗在窗口的两端都为0，杜绝了所有不连续性。 Hamming窗的窗口两端不为0，信号中仍然会呈现不连续性。 Hamming窗擅长减少最近的旁瓣，但是不擅长减少其他旁瓣。 Hamming窗和Hanning适用于对频率精度要求较高对旁瓣要求较低的噪声测量。 ”**

![img](https://tva1.sinaimg.cn/large/007S8ZIlgy1ggt4xrfianj30k50d3js8.jpg)

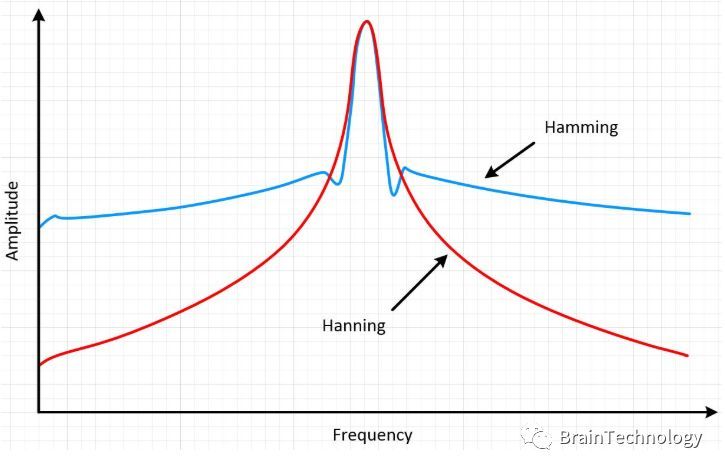
**图 Hamming和Hanning都会产生宽波峰低旁瓣的结果**

![img](https://tva1.sinaimg.cn/large/007S8ZIlgy1ggt4xv5biej309l07ft91.jpg)

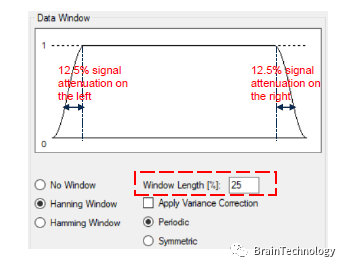
**Hanning窗适用于95%的情况。 它不仅具有较好的频率分辨率，还可减少频谱泄露。 如果您不知道信号特征但是又想使用平滑窗，那么就选择Hanning窗。**

**Analyzer软件中的实现**

#### **谢谢大家观看，如有帮助，来个喜欢或者关注吧！**

本文作者：Chen Rui

星球地址 ：[知识星球](https://t.zsxq.com/W5M3F)[Blog ](https://t.zsxq.com/W5M3F)

知乎地址 : [知乎专栏](https://www.zhihu.com/people/braintechnology) 

B站地址 : [B站主页](<https://space.bilibili.com/328549846 >)&#x20;

公众号：大脑技术\
&#x20;CSDN地址 : [csdn主页](https://blog.csdn.net/craig_cc)